There are arbitrage opportunities when the value of puts and calls on the same stock fall out of line, reports Alan Ellman.
Put–call parity is a principle that defines the relationship between the price of European put options and European call options of the same stock, strike price and expiration date. The formula can identify arbitrage opportunities where the simultaneous buying and selling of securities and options result in reduced-risk opportunities.
I am writing this article in response to a number on inquiries why I have rarely addressed this topic in the past. The subject is a bit complicated and doesn’t directly impact our option-selling trades but is an important concept vis-à-vis options pricing and education. So here we go.
Put-Call Parity formula
Stock price at expiration + put value at expiration = call value at expiration + face value of a bond that will pay for exercise of the call option at expiration.
Think of each side of the equation as an individual portfolio and, if put-call parity is respected, both portfolios will be of equal value at contract expiration. If not, an arbitrage opportunity will exist.
Assumptions in this formula
Apply only to European style options that can be exercised only at contract expiration
- Transaction costs not included
- Dividends not included
- Adequate liquidity available
- Same stock
- Same expiration
Put-Call parity with no arbitrage opportunity (data for calculations in far right column)
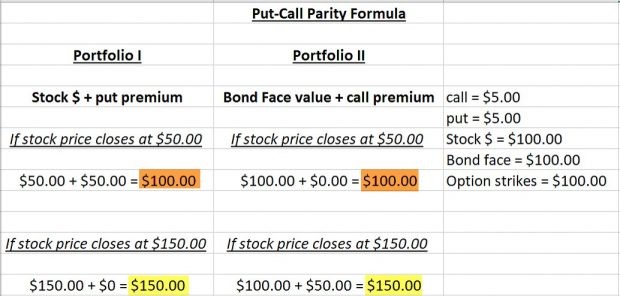
Put-Call Party: No Arbitrage Opportunity
Each side of the equation or portfolio expires with equal value
Put-Call parity with arbitrage opportunity
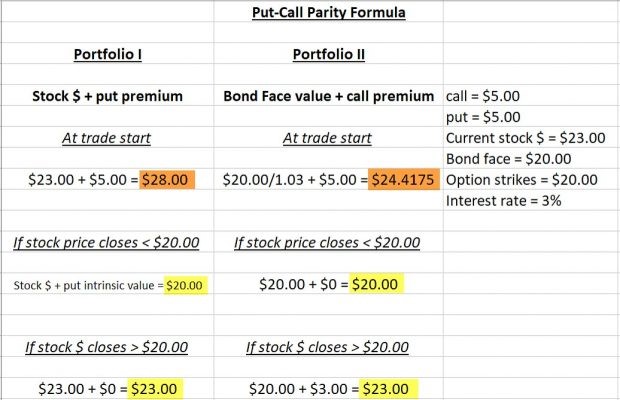
Put-Cal Parity: Arbitrage Opportunity
We used an interest rate of 3% just to complete the formula. The reason we use $20.00/1.03 for the bond value at the start of the trade is because the face value of $20 is not realized until contract expiration so the 3% interest rate must be accounted for. Note that in the brown cells the arbitrage opportunity was identified but in the yellow cells the inflows in both portfolios was the same whether share price moved up or down. The market immediately eliminates these arbitrage opportunities which apply only to institutional investors.
How do institutional traders make money when arbitrage opportunities are identified?
The more expensive portfolio is sold and the cheaper portfolio is purchased. In this scenario, a profit of $3.5825 per share will be a risk-free return. They manage their trades via shorting stocks and writing puts but this is not relevant to retail investors.
Discussion
Arbitrage opportunities are not applicable to retail investors because we don’t have the tools to identify them fast enough when they occur. Since this was a topic of interest to many in our BCI community, I decided to publish. While this may not be applicable for retail, understanding how it works is key to understanding options pricing.
Use the multiple tab of the Ellman Calculator to calculate initial option returns (ROO), upside potential (for out-of-the-money strikes) and downside protection (for in-the-money strikes). The breakeven price point is also calculated. For more information on the PCP strategy and put-selling trade management click here and here. I'll be presenting a free, one-hour webinar for the Options Industry Council on Wednesday May 8 at 3:30 p.m. CST, entitled, Covered Call Writing: Basics and Practical Application. The event is open to all. Just follow the link above to register.
Even if you feel you may not be able to attend the live presentation, sign up and receive a recording to review at your leisure.



















