Two strategies for trading volatility are straddles and strangles, which are also very risky, so Russ Allen of Online Trading Academy details an alternative that is similar but also limits risk.
Recently I’ve been writing here about straddles and strangles. These are the most well-known and straightforward strategies (but not necessarily the best ones) for situations where we believe that:
- There will be a large change in the price of the underlying asset, which could be in either direction.
- Implied volatility is very low, and therefore likely to rise.
Since we are neutral as to the direction of price movement, our strategy should be initially delta-neutral, or at least roughly so. We believe that Implied Volatility will rise, so we want our strategy to have positive Vega. Because we believe that price will move sharply, our strategy should have a positive gamma. Positive gamma strategies benefit from price moving; negative gamma strategies benefit from price sitting still. Any strategy with a positive gamma must necessarily have a negative theta. It’s a rule. The more price movement helps us, the more time hurts us. We’ll have to live with it.
Last week we extended our example where this was our opinion, using the exchange-traded fund called XLF. XLF is an ETF representing a basket of stocks in the financial industry. We compared a straddle and a strangle in some detail, and demonstrated that the strangle was a more highly-leveraged bet than the straddle. The strangle pays off better if we get either a big change in price (up or down); or a big increase in IV; or both. The strangle would also lose more if a big change did not happen. The choice came down to just how confident we were that there would in fact be a big change. The more confident we were, the more the advantage would go toward the strangle.
The problem is, both straddles and strangles are extremely risky trades—in fact, they are some of the riskiest option trades you can make. The race of price and volatility against time is never a sure bet. But there are other alternatives, which we should now be in a position to understand.
I mentioned at the end of last week’s article that an alternative strategy called a backspread could also be used in a similar situation. This will be good news to those of you who have heard all you want to hear about straddles and strangles! Thanks for bearing with me up to now—we needed to clearly understand the mechanics behind those strategies before we move on.
NEXT PAGE: The Ratio Backspread |pagebreak|
So let’s talk about the backspread, which is also called a ratio backspread. This is a limited-risk strategy (no naked short options); which benefits from a large increase in volatility (high positive vega); while also benefiting from a movement in the underlying price away from a certain single price point (initially delta neutral, with positive gamma). Since the position initially has positive gamma (price movement helps it), it therefore must have negative theta, and it does. So far, it sounds very much like a straddle.
Before we get into the mechanics of doing a backspread, here are the functional differences between a backspread and a straddle:
- A straddle has unlimited profit in both directions; a backspread’s profit is unlimited on one side only, and limited on the other side.
- A straddle is always initiated for a fairly large debit. A backspread will cost less, and can often be done for a credit (although there will be a margin requirement, which will be roughly similar to the cost of the straddle).
- A backspread will normally decay more slowly (smaller negative Theta).
- A backspread will usually lose a smaller percentage of its margin if it’s wrong.
- A backspread needs less price movement to move into profitable territory.
- A backspread is generally less sensitive to changes in implied volatility (smaller vega).
- A backspread wins a smaller percentage of its cost if it’s right.
Altogether, we can say in general that if we want a delta-neutral, positive-gamma, positive-vega strategy, a backspread is a lower-risk, somewhat lower-reward choice than a straddle. In many cases, it will be the better choice.
Backspreads involve either all puts (a put backspread), or all calls (a call backspread). First, note that either type initially profits from a move in either direction, just like a straddle. But profits for put backspreads are unlimited to the downside and limited to the upside, while profits for call backspreads are limited down, unlimited up.
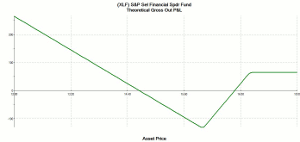
The payoff diagram of a put backspread always has a shape similar to that shown in Figure 1. Note the V-shaped portion, which is similar to a straddle. Also note that profit is limited to the upside. A call backspread’s diagram looks similar but flipped side to side, with the downside the limited direction.
Here’s how a backspread is constructed. Whether we use puts (for a bearish bias) or calls (for a bullish bias), we buy a certain number of contracts at one strike price; and simultaneously sell a smaller number of contracts at a more-expensive strike price (the short strike is higher than the long strike for puts, and it’s lower for calls). The position’s profile is similar to a straddle over a certain range of prices, with the bottom of the V at the strike price of the long contracts. The diagram indicates that profit goes flat at the strike price of the short contracts.
NEXT PAGE: A Concrete Example |pagebreak|
For example, with XLF, on December 14 we could have initiated a put backspread by buying three March 16 puts at $.63; and simultaneously selling two March 17 puts at $1.27. The March 16’s would cost us $63 per contract, or $189 for the three in total. Selling the 17’s would bring in two times $127, or $254. Altogether, the net result would be a credit to our account of $65.
Buying the 16-strike puts pegged $16 as the price we wanted/expected the underlying price to move away from (same as when we bought the 16 puts as part of the straddle). This makes sense—the price was right at $16 at the time, and we expected a move away from there.
Selling the two 17-strike puts (which were in the money and therefore more expensive) brought in enough money to pay for the three 16-strike puts, and provide a $65 credit besides (Yay!). The short 17-strike puts are what give us our profit to the upside. Every penny of value they lose goes into our pocket. The more price moves up, the less they’ll be worth.
But they can’t be worth less than zero. That’s why our profit to the upside is limited. All of it comes from a decline in value of the 17 puts. If we held this position to expiration, at any underlying price above 17, all the puts, both our long 16’s and the short 17’s, expire worthless. In that case, everything vanishes except the initial $65 credit in our account.
On the other hand, if XLF moves down in a big way, our profit is unlimited. Although we’re short two of the 17 puts, we’re long three of the 16’s. At an XLF price of $12.00 at expiration for example, our two short 17 puts would be worth ($17-12) X 2 X 100 = $1,000, which we’d have to pay. But our three long 16 puts would be worth ($16-12) X 3 X 100 = $1,200. Our profit would be $1,200 - $1,000 = $200, plus the original credit of $65, for a total of $265. For every dollar that XLF falls beyond that, we’re losing another $200 on the 17’s while making another $300 on the 16’s, for an additional net profit of $100 per point of price drop.
Last thing for this week—we will usually not hold a backspread until expiration. A major point of it is to benefit from an increase in implied volatility. Since IV only has any meaning when there is time value, that means selling our long options while they still have considerable time value. Next time, we’ll continue with our analysis of backspreads, focusing on the effects of changing IV.
By Russ Allen, Instructor, Online Trading Academy